Vorwort Zu aller erst einmal "Vielen Dank" das Sie sich für das Spiel SUDOKU interessieren und die Absicht haben es zu spielen. Das freut mich sehr. An dieser Stelle möchte ich mich bei allen Helfern bedanken die später noch in den Credits genau erwähnt werden. Ohne sie wäre es nicht einfach gewesen das Spiel so zu erstellen wie Sie es heute vor sich haben. Auch wenn es sich hierbei um ein kleines Spiel handelt, wurde doch einiges an Arbeit geleistet. Sofern Sie SUDOKU regelmäßig spielen wollen würden wir uns sehr freuen, wenn Sie diese Leistung mit einem kleinen Obolus honorieren würden. Hierfür haben wir bei PayPal einen entsprechenden Account eingerichtet. Sie können das Geld direkt über die Adresse paypal@silicon-wizards.com anweisen oder verwenden Sie den entsprechenden Button auf dieser Seite. Die Höhe des Betrages ist gänzlich Ihnen überlassen - wir freuen uns über jede Kleinigkeit. Installation Systemvoraussetzungen Benötigt wird ein AMIGA OS3.1 kompatibler Computer mit Picasso96 oder CGX V4 kompatiblem Grafiksystem sowie ein AHI kompatibles Audiosystem. Die Grafikkarte muss einen Bildschirm in der Größe 800 x 600 Pixel mit 15/16 bit Farbtiefe erzeugen können. Für den Start des Spieles sind 20 MB freier Hauptspeicher notwendig. Installation Entpacken Sie das Archiv an eine beliebige Stelle. Sofern noch nicht vorhanden kopieren Sie bitte die beiden Bibliotheken ttengine.library und mpega.library aus dem libs Verzeichnis nach LIBS:. SUDOKU starten Das Hauptmenu Nach dem Intro befinden Sie sich im Hauptmenu. Hier können Sie ein neues Spiel starten, die Credits aufrufen oder das Spiel beenden. Wenn Sie ein neues Spiel starten erscheint als nächstes die Auswahl des Schwierigkeitsgrades. 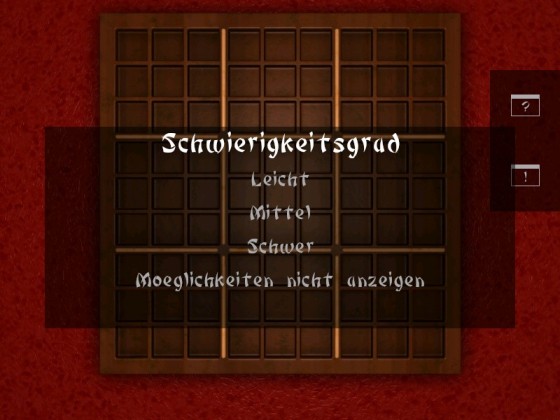Der Schwierigkeitsgrad Jedes Mal wenn Sie ein neues Spiel Starten (über das Hauptmenu oder das Spielmenu) können Sie die Schwierigkeit des nächsten Spieles festlegen. Sie haben die Auswahl zwischen Leicht, Mittel und Schwer. Je nachdem für welche Stufe Sie sich entscheiden sind mehr oder weniger Felder nicht belegt und müssen gelöst werden. Außerdem haben Sie noch die Option, sich die Möglichkeiten der einzelnen Felder anzeigen zu lassen. Sie sehen dann direkt in jedem einzelnen Feld, welche Zahlen dort möglich wären. Standardmäßig ist diese Option ausgeschaltet, was die Schwierigkeit erhöht. SUDOKU spielen       Während dem Spiel wählen Sie durch einen Linksklick auf ein leeres Feld dieses aus. Das Augewählte Feld wird rot markiert. Daraufhin werden Ihnen die möglichen Zahlen links neben dem Spielbrett angezeigt. Je nachdem ob Sie beim Spielstart die Option "Möglichkeiten anzeigen" gewählt haben, werden ihnen nur die tatsächlichen Möglichkeiten angezeigt. Ansonsten bekommen Sie alle Zahlen von 1-9 angezeigt aus denen Sie wählen können. Mit einem Linksklick auf eine dieser Möglichkeiten wählen Sie ihre Zahl aus. Ein Rechtsklick schließt die Zahl aus. Ob Ihre Wahl richtig oder falsch ist, wird ihnen am unteren Bildschirmrand angezeigt. Wenn Sie die Option "Möglichkeiten anzeigen" gewählt haben, können Sie mit den Zifferntasten Ihrer Tastatur (1-9) die jeweilige Zahl grün hervorheben. Die Taste 0 markiert alle Päärchen auf dem Spielfeld. Tipp: Sollten nur die tatsächlichen Möglichkeiten angezeigt werden und daher nur eine einzige Zahl in dem von Ihnen ausgewählten Feld möglich sein, so können Sie diese mit einem einfachen Doppelklick in das Feld einfügen. Die Hilfe < Wenn Sie das Fragezeichen auf der rechten Seite auswählen, bekommen Sie eine kleine Hilfestellung vom Spiel. Entweder wird eine Zahl aufgedeckt (an der Stelle wird ein blinkendes Fragezeichen dargestellt) oder es werden Möglichkeiten ausgeschlossen (diese werden mit einem "X" gekennzeichnet). Ein entsprechender Text weist auf die Art der Lösung hin. Optionen Das Ausrufezeichen öffnet das Spielmenu. Hier können Sie ein neues Spiel starten oder zum Hauptmenu zurückkehren wo Sie z.B. das Spiel wieder beenden können. Sollten Sie das Menu aus versehen aktiviert oder es sich anders überlegt haben, können Sie das Spiel auch einfach fortsetzen. Ziel des Spieles / Spielregeln Ziel des Spieles Das Ziel des Spieles besteht darin, dass man alle leeren Felder mit gültigen Zahlen füllt. Sobald dies geschafft ist, ist das Spiel beendet. Spielregeln Das Spiel besteht aus einem 9x9 Felder großen Spielbrett das in 3x3 Blöcken unterteilt ist. Die Regel zum Füllen der Felder ist sowohl einfach als auch schwierig. Jede Zeile, jede Spalte und jeder Block muss alle Zahlen von 1-9 enthalten. Was auch bedeutet, dass jeweils nur eine Zahl pro Zeile, Spalte oder Block vorkommen darf. Bei der Lösung eines Feldes darf nicht geraten werden. Ein Feld darf nur mit einer Zahl belegt werden, wenn Sie eine eindeutige Wahl treffen können. Können Sie das nicht, müssen Sie sich einem anderen Feld widmen. Eventuell hilft Ihnen das ja weiter. Jedes SUDOKU hat von Natur aus nur eine gültige Lösung. Um einer Lösung näher zu kommen stehen Ihnen in den folgenden Abschnitten diverse Lösungshilfen zur Seite. Lösungshilfen Grundlagen Um der Lösung eines Feldes näher zu kommen hilft es festzustellen, welche Zahlen in diesem Feld möglich sind. Hierzu können sie alle Zahlen ausschließen die schon in anderen Feldern der Zeile, Spalte oder des Blocks verwendet werden. Nachdem Sie das gemacht haben bleiben nur noch die wirklichen Möglichkeiten übrig. Tipp: Diese Tätigkeit übernimmt SUDOKU für Sie, wenn Sie bei der Wahl des Schwierigkeitsgrades "Möglichkeiten anzeigen" ausgewählt haben. Einzelfelder Bei jeder Zelle die nur eine Möglichkeit zur Lösung bietet kann diese Zahl problemlos eingesetzt werden. Bitte achten Sie darauf, dass diese Zahl bei den Möglichkeiten der anderen Felder dieser Zeile, Spalte und des Blocks ausgeschlossen wird. 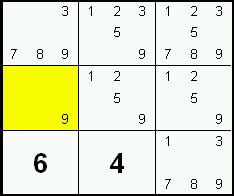Tipp: Wenn Sie bei der Wahl des Schwierigkeitsgrades "Möglichkeiten anzeigen" ausgewählt haben, aktualisiert SUDOKU nach jedem einsetzen einer Zahl die Möglichkeiten der Felder. 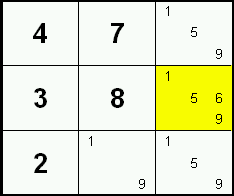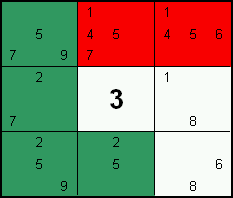Verstecktes Einzelfeld Wenn eine Zahl nur in einem Feld einer Zeile, Spalte oder Block möglich ist, dann ist das die Lösung. In diesem Beispiel ist die Zahl 6 nur im mittleren Rechten Feld möglich. Da jeder Block eine 6 besitzen muss, gehört die Zahl in dieses Feld. Die oben genannten Möglichkeiten sind die einzigen, die sofort zu einer Lösung führen. Oft können diese Lösungsmöglichkeiten allerdings nicht angewandt werden. In einem solchen Fall ist es notwendig die Möglichkeiten der einzelnen Felder zu reduzieren um früher oder später ein Einzelfeld oder verstecktes Einzelfeld zu ermitteln. Hierzu dienen die folgenden Lösungshilfen. Blockierte Kandidaten (1. 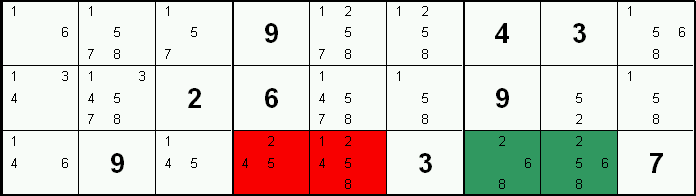Fall) Manchmal kommt es vor, dass eine Zahl innerhalb eines Blockes nur in einer Zeile oder Spalte vorkommt. Da diese Zahl auf jeden Fall in dieser Zeile oder Spalte gesetzt wird, können nun die Zahlen der Zeile oder Spalte außerhalb dieses Blocks ausgeschlossen werden. In diesem Beispiel besteht für den rechten Block nur in der untersten Zeile die Möglichkeit eine 2 einzusetzen (grüne Markierung). Da eine der beiden Felder auf jeden Fall eine 2 sein muss, können die übrigen Zweien des mittleren Blocks der gleichen Zeile (rote Markierung) ausgeschlossen werden. Blockierte Kandidaten (2. Fall) Manchmal kommt es vor, das eine Zahl innerhalb einer Zeile oder Spalte auf einen Block beschränkt ist. In diesem Fall kann diese Zahl aus den anderen Feldern des Blocks ausgeschlossen werden. In diesem Beispiel sind die Neunen der linken Spalte auf den mittleren Block beschränkt (grüne Markierung). Da die Spalte auf jeden Fall Neunen benötigt, muss eins der beiden Felder eine Neun sein. Demnach können die übrigen Neunen des Blocks (rote Markierung) ausgeschlossen werden. 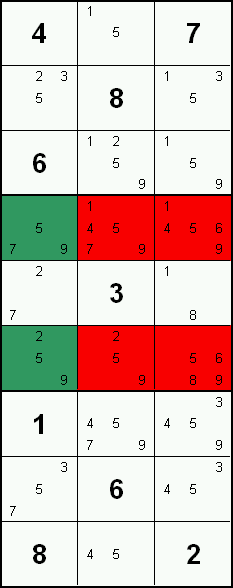Offene Paare Wenn 2 Felder einer Gruppe (Zeile, Spalte, Block) ein identisches Paar Zahlen enthalten (und nur diese beiden Zahlen), dann können diese beiden Zahlen in keinem anderen Feld der Gruppe auftreten. Somit können diese beiden Zahlen aus den anderen Feldern der Gruppe ausgeschlossen werden. In diesem Beispiel stehen in den Spalten 6 und 7 das offene Pärchen 6 und 8 (grüne Markierung). Demzufolge können die Sechsen und Achten der anderen Felder (rote Markierung) ausgeschlossen werden. Offene Dreier Ein offener Dreier tritt auf, wenn sich drei Felder einer Gruppe drei Zahlen (und sonst keine weiteren) teilen. Wobei nicht jede der drei Zahlen auftreten muss. Sofern diese drei Zahlen in anderen Feldern der Gruppe auftreten, können diese dort ausgeschlossen werden. In diesem Beispiel besteht der offene Dreier mit den Zahlen 1, 4 und 6 aus den Feldern "oben Links", "unten links" und "unten rechts" (grüne Markierung). Demnach können die übrigen Einsen, Vieren und Sechsen ausgeschlossen werden (rote Markierung). Offene Vierer Einen offenen Vierer sehen Sie, wenn sich vier Felder einer Gruppe außer 4 bestimmten Zahlen keine weiteren Zahlen teilen. Wobei auch hier wieder nicht jede Zahl in jedem Feld auftreten muss. In diesem Beispiel finden Sie die Zahlen 2, 5, 7 und 9 in den linken Feldern und unten in der Mitte (grüne Markierung). Diese bilden den offenen Vierer. Also können die restlichen Fünfen und Siebenen ausgeschlossen werden (Rote Markierung). 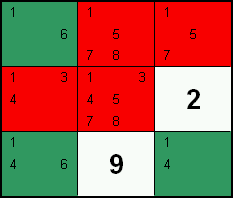Versteckte Paare Wenn 2 Felder einer Gruppe ein identisches Paar enthalten und diese Zahlen in keinem anderen Feld der Gruppe auftreten, können alle weiteren Zahlen der beiden Felder ausgeschlossen werden. In diesem Beispiel existieren die beiden Zahlen 1 und 9 nur in den markierten Feldern und stellen somit das versteckte Paar dar. Da also eins der Felder die 1 und das andere die 9 sein muss können die restlichen Zahlen (also die 2 und die 5) aus diesen Feldern ausgeschlossen werden. 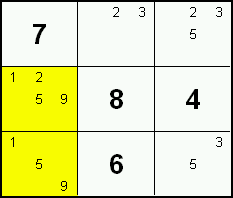Versteckte Dreier Wenn 3 Zahlen nur in 3 Feldern einer Gruppe vorkommen, können alle weiteren Zahlen innerhalb dieser 3 Felder ausgeschlossen werden. In diesem Beispiel gibt es die Zahlen 3, 6 und 7 nur in den Spalten 4, 6 und 7. Demnach können alle anderen Zahlen (1, 2, 4 und 9) aus diesen Feldern ausgeschlossen werden. Tipp: Versteckte Dreier sind oftmals schwierig zu finden. Glücklicherweise werden sie selten zum Lösen eines Sudokus benötigt. X-Wing Man geht von einer spezifischen Zahl aus. Wenn nun diese Zahl als Möglichkeit nur zwei mal in zwei Zeilen vorkommt und diese Felder sich auch noch 2 Spalten teilen, formen diese einen X-Wing. Dementsprechend formen 2 Spalten mit jeweils 2 Zahlen die sich 2 Zeilen teilen ebenfalls einen X-Wing. Diese 4 Felder sind die einzigen Möglichkeiten wo die Zahl innerhalb der Zeilen und Spalten vorkommen kann. Jede weitere Möglichkeit innerhalb der jeweiligen Spalte oder Zeile (welche 2 von diesen Eckpunkten enthält) kann somit ausgeschlossen werden. In diesem Beispiel werden nur die Sechsen als Möglichkeiten angezeigt (gefiltert). Die blauen und grünen Markierungen zeigen den X-Wing, da die Zeilen 1 und 9 nur zweimal die 6 als Möglichkeit enthalten und außerdem noch ein Rechteck darstellen (sie teilen sich 2 Spalten). Bitte beachten sie, dass nur die blauen oder die grünen Felder später mal eine 6 enthalten können. Demnach können die übrigen Sechsen der beiden Spalten 6 und 9 (rote Markierung) ausgeschlossen werden. 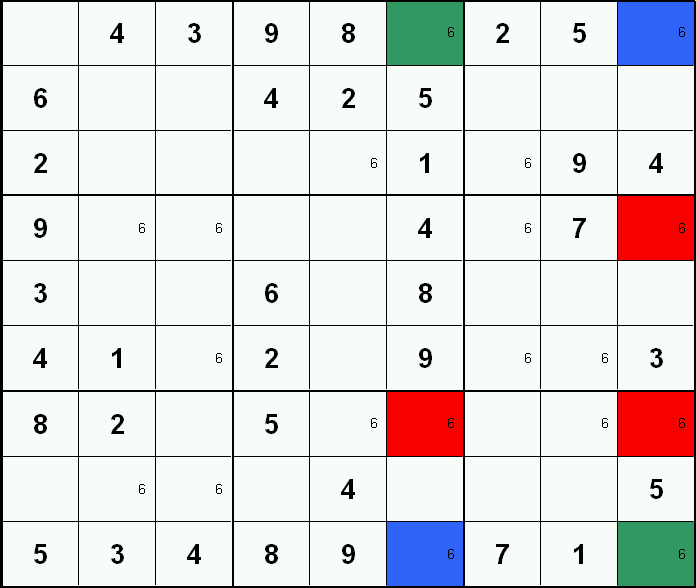Schwertfisch Der Schwertfisch ist eine Erweiterung des X-Wings. Man geht wiederum von einer spezifischen Zahl aus. Ein Schwertfisch besteht aus 3 Zeilen die jeweils nicht mehr als 3 Mal die Möglichkeit der betrachteten Zahl enthalten. Alle drei teilen sich die gleichen 3 Spalten. Natürlich funktioniert das auch mit 3 Spalten zu je max. 3 Feldern die sich 3 Zeilen teilen. Diese Felder formen ein Gitter aus 9 Feldern, die die einzigen möglichen Positionen der betrachteten Zahl innerhalb dieser Zeilen und Spalten darstellen. In diesem Beispiel werden nur die Fünfen als Möglichkeit angezeigt. 3 Spalten (2, 5 und 8) verfügen über max. 3 Felder (in diesem Fall sind es nur 2) mit der Zahl 5 als möglichen Inhalt (grüne Markierung). Diese 3 Spalten teilen sich 3 gemeinsame Zeilen (1, 4 und 9). Dies stellt einen Schwertfisch dar. Andere Felder innerhalb der betrachteten Zeilen mit der 5 als Möglichkeit können somit ausgeschlossen werden (rote Markierung). 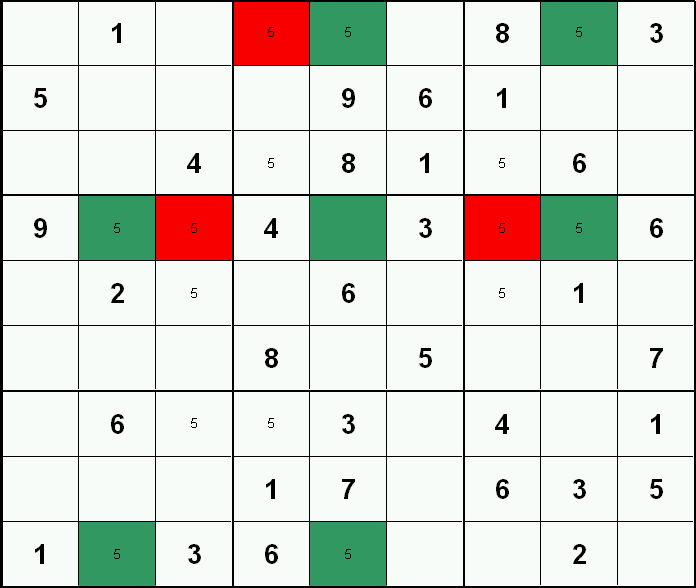Tipp: Bitte beachten sie, dass (wie in diesem Beispiel gezeigt) nicht immer 3 Felder pro Zeile oder Spalte bestückt sein müssen. Oftmals sind es nur 2. Lösung mit Farben Hier werden die Möglichkeiten betrachtet, die nur in 2 Feldern einer Gruppe auftreten. Diese beiden Felder haben eine Paarbeziehung in der entweder der eine oder der andere die richtige Position der Möglichkeit ist. Da wir noch nicht wissen, wer von beiden der "Richtige" ist, stellen wir das ganze mit zwei verschiedenen Farben dar. Typischerweise existieren gleich mehrere solcher Paare während des Spielverlaufs. Manchmal kommt es vor, dass solche Paare mit weiteren Paaren über eine Kette von "Richtig" und "Falsch" verbunden sind. Dies kann dazu führen, dass andere Möglichkeiten ausgeschlossen werden können. Wann immer zwei Felder einer solchen Paarkette die gleiche Farbe besitzen und sich eine Gruppe teilen muss diese Farbe "Falsch" sein, da jede Gruppe nur einmal die betrachtete Zahl enthalten darf. Sollten außerdem Felder außerhalb dieser Paarkette in Bezug zu einem der Paare stehen kann diese Möglichkeit ausgeschlossen werden. In diesem Beispiel wurden nur die Fünfen angezeigt. Die Felder A und B bilden eine Paarbeziehung, da dies die einzigen beiden Möglichkeiten für eine 5 in der Zeile 8 sind. Außerdem bildet B noch eine Beziehung mit C, da sie die einzigen Möglichkeiten einer 5 in diesem Block darstellen. Schlussendlich formen C und D ebenfalls ein Paar, da sie die einzigen Möglichkeiten in der Zeile 8 repräsentieren. Da diese 3 Paarbeziehungen eine Beziehungskette bilden, können wir sie farblich markieren (blau und grün) und somit genauer betrachten. Die rote Markierung zeigt eine 5 die in Beziehung zu der Kette steht (Feld A und D). Da A oder D auf jeden Fall eine 5 sein müssen, kann diese Möglichkeit somit ausgeschlossen werden. 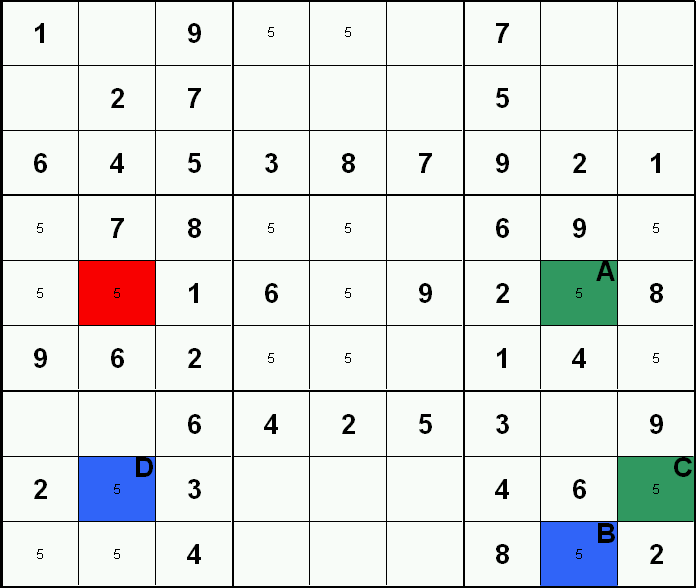Credits Idee und Programmierung Michael Lanser Grafik Markus Lanser Musik und SoundFX Frank Schlick Übersetzer Stefan Geese, Stefanie Kloss, Sébastien Ligez Betatester Dieter Groppé, Oliver Eschbach, Heinz Süss Copyright 2006 by Silicon Wizards