Preamble At first a big "Thank You" for your interest in the game SUDOKU and your intention to play it. At this place I would like to thank all helpers which are mentioned in the credits. Without them this game wouldn't be as it is today. Even if this is a small game it needed considerable work. So if you want to play SUDOKU regular we would be pleased if you honor us with a small mite. Therefor we set up a PayPay account. You can send the money directly to paypal@silicon-wizards.com or use the corresponding button on this page. The amount is let to you - we are happy about every penny. Installation System requirements To play this game you need a computer compatible to AMIGA OS3.1 and a Picass96 or CGX V4 compatible graphics system and a AHI compatible audio system. Your graphics gard must be able to display pictures at 800 x 600 pixel at a color depth of 15/16 bit. Furthermore 20 MB of free memory is needed. Installation Unpack the archive to a custom destination and copy the ttengine.library and mpega.library from the libs directory to LIBS: if they are not already there. Start SUDOKU The Main Menu After the intro you are located in the main menu. Here you can start a new game, enter the credits or quit the game. When a new game is started you have to choose the difficulty level. 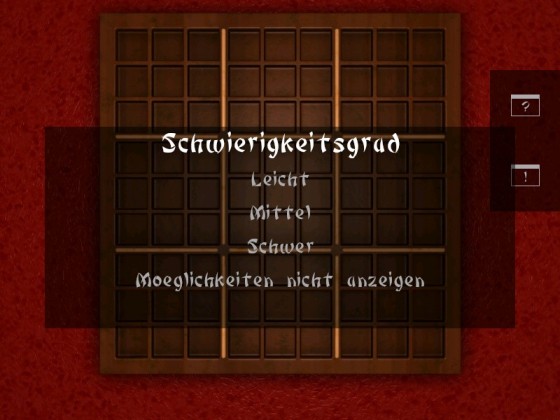The Difficultylevel Each time a new game is started (during the main menu or the game menu) you can choose the difficulty level for the next game. Easy, Medium and Hard are available. Depending on what you choose there are more or less fields empty and have to be solved. In addition you have the option to let you show the real possibilites for a field. The posibilities will be shown inside of every empty field. This option is not active by default. Play SUDOKU       During the game you choose an empty field by left clicking it. The field will be marked red. Herupon you get the possible numbers shown on the left side of the board. If you choosed the option "show possibilities" only the numbers will be shown which could match into this field. Otherwise you can choose out of every number from 1 to 9. A left click on such a number chooses it and a right click eliminates it. If your choice was right or not will be shown at the bottom of the board. If you choosed the option "show possibilities" you can highlight every possibility by pressing the keys 1-9. Pressing the 0 highlights the pairs. Tip: When only the real possibilities are shown and therefor only one number can match into the filed a double click on the field fills the number. Help The question mark on the right side of the board symbolises the help. After activating it you get a field filled (a blinking question mark appears on the field) or some possibilites will be eliminated (a blinking "X" appears). You will get a note at the bottom explaining what help was provided. Options The exclamation mark activates the game menu where you can either start a new game or return to the main menu (where you can quit the game). If you have clicked this symbol accidentally, there is certainly one menu point to continue the game. Objective / Rules Objective To win the game you have to fill all empty fields. When there are no more empy fields left, you win the game. Rules The game consists of a 9x9 fields board divided into 3x3 blocks. Some fields are already filled at the beginning of the game. The rules to fill the empty fields are as easy as hard. Each row, each column and each block must contain the numbers 1 to 9. This also means that every number has to be unique in every row, column and block. To solve such a field you don't have to guess. You only have to fill a field when your choice is clear-cut. If your choice is not clear you have to look at another field. Probably this one can help you. Every SUDOKU has only one valid solution. To help you in solving a SUDOKU the following chapters could be helpful. Solving Tips Basics Firstly, it's impossible to get very far without carefully maintaining a list of 'possible values' or candidates for each blank cell. So you would need to analyse each blank cell - starting with the assumption it can have any value between 1 and 9, then removing all values which have already been assigned to other cells in its respective row, column and block. This leaves each blank cell with a list of candidates. Tip: If you choosed "show possibilities" while selecting the difficulty level, SUDOKU will update the possibilites for you automatically. Singles Any cells which have only one candidate can safely be assigned that value. It is very important whenever a value is assigned to a cell, that this value is also excluded as a candidate from all other blank cells sharing the same row, column and block. Tip: If you choosed "show possibilities" while selecting the difficulty level, SUDOKU will update the possibilites for you automatically. 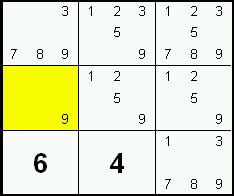Hidden Single Very frequently, there is only one candidate for a given row, column or block box, but it is hidden among other candidates. In this example, the candidate 6 is only found in the middle right cell of the block. Since every block must have a 6, this cell must be that 6. While the steps above are the only ones which will directly assign a cell value, they will only solve the simplest puzzles. That's fortunate, otherwise Sudoku wouldn't be as popular as it is today. The following steps (in increasing complexity) will reduce the number of candidates in blank cells so, sooner or later, a 'single' candidate or 'hidden single' candidate will appear. 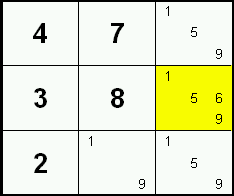Locked Candidates 1 Sometimes a candidate within a block is restricted to one row or column. Since one of these cells must contain that specific candidate, the candidate can safely be excluded from the remaining cells in that row or column outside of the block. In this example, the right block only has candidate 2's in its bottom row (green mark). Since, one of those cells must be a 2, no cells in that row outside that block can be a 2. Therefore 2 can be excluded as a candidate from the red marked cells. 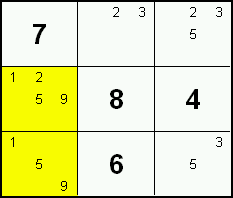Locked Candidates 2 Sometimes a candidate within a row or column is restricted to one block. Since one of these cells must contain that specific candidate, the candidate can safely be excluded from the remaining cells in the block. In this example, the left column has candidate 9's only in the middle block (green mark). Therefore, since one of these cells must be a 9 (otherwise the column would be without a 9), 9's can safely be excluded from all cells in this middle block except those in the left column (red mark). 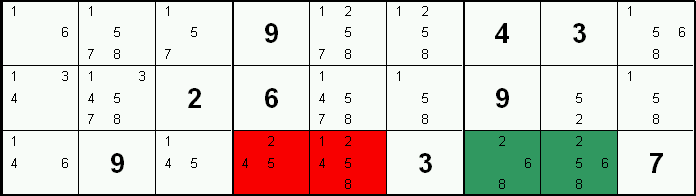Naked Pairs If two cells in a group (row, column, block) contain an identical pair of candidates and only those two candidates, then no other cells in that group could be those values. These 2 candidates can be excluded from other cells in the group. In this example, the candidates 6 & 8 in columns six and seven (green mark) form a Naked Pair within the row. Therefore, candidates 6 & 8 can be excluded from other cells in the row (red mark). Naked Triples A Naked Triple occurs when three cells in a group contain no candidates other that the same three candidates. The cells which make up a Naked Triple don't have to contain every candidate of the triple. If these candidates are found in other cells in the group they can be excluded. In this example, a Naked Triple is formed by the top left, bottom left & bottom right cells of a block (green mark) since they only contain the candidates 1, 4 & 6. Therefore the candidates 1 & 4 in the red marked cells can be excluded safely. 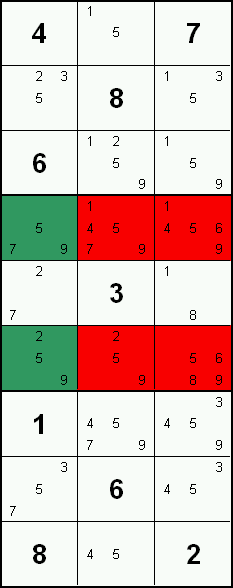Naked Quads A Naked Quad occurs when four cells in a group contain no candidates other that the same four candidates. The cells which make up a Naked Quad don't have to contain every candidate of the quad. In the example on the right, the candidates 2, 5, 7 & 9 in the 3 left most cells and bottom middle cell of a block (green mark) form a Naked Quad. Therefore candidates 5 & 7 that are in the red marked cells can be excluded. 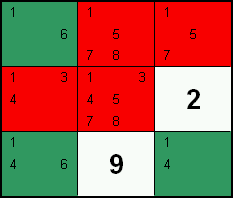Hidden Pairs If two cells in a group contain an identical pair of candidates and no other cells in that group contain those 2 candidates, then other candidates in those two cells can be excluded safely. In this example, the candidates 1 & 9 are only located in two highlighted cells of a block, and therefore form a pair. All candidates except 1 & 9 can safely be excluded from these two cells as one cell must be the 1 while the other must be the 9. 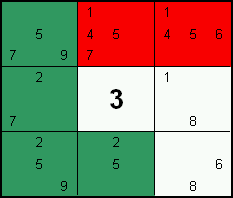Hidden Triples If three candidates are restricted to three cells in a given group, then all other candidates in those three cells can be excluded. In this example, the candidates 3, 6 and 7 are found only in column four, six and seven. Therefore, all other candidates can be excluded from those three cells. Tip: Hidden triples are generally very hard to spot but fortunately they're rarely required to solve a puzzle. X-Wing Given a specific candidate - the X-Wing pattern requires two rows containing two cells (and only two cells) with this candidate in each row, and these candidates must share the same 2 columns forming a rectangular 'X-Wing'. Likewise, two columns with two cells (and only two cells) containing this candidate in each column sharing 2 rows also form an X-Wing. These four cells are the only possible locations for 'true' candidates in these 2 rows and columns. Any candidates in a group containing two corners of this X-Wing (except the 'corner' cells themselves) can safely be excluded. In this example filtering has been added so only candidate 6's are visible. The blue and green cells form a classic "X-Wing" since rows one and nine both have only two cells with candidate 6's and they form a rectangle (ie sharing 2 columns). Note: either the blue cells or the green cells represent the 'true' candidate. Therefore, other candidate 6's in columns six and nine (highlighted red) can safely be removed as these columns contain a blue and green 'corner' cell. 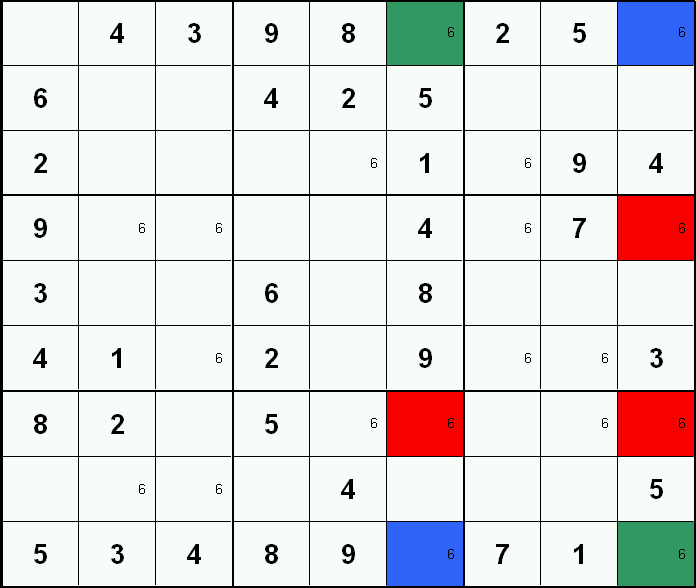Swordfisch The Swordfish pattern is a variation on the "X-Wing" step above. Given a specific candidate, a Swordfish pattern is formed by three rows each containing no more than three cells with the candidate and all sharing the same three columns. Likewise, three columns each containing no more than three cells with the candidate and all sharing the same three rows will form a Swordfish pattern. These cells form a grid of nine cells which are the only possible locations for 'true' candidates in these 3 rows and columns. Any candidates in a group containing three 'grid cells' (except the 'grid cells' themselves) can safely be excluded. In this example, filtering has been added so only candidate 5's are visible. Three columns (two, five & eight) have candidate 5 in no more than three cells (two cells each in this case), and these cells all share the same three rows (one, four & nine). A "Swordfish" pattern is established (green mark). Other cells with candidate 5 within this grid (red mark) can be excluded safely. 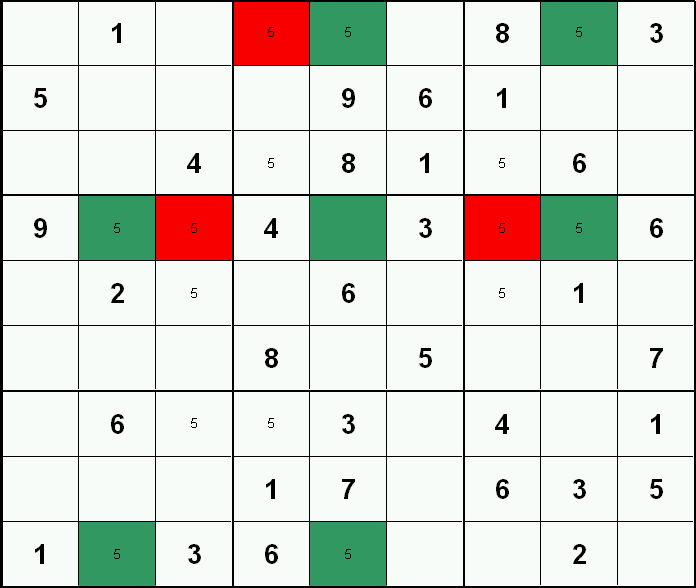Tip: Remember: as shown in this example, there does not have to be 3 cells in each row (or column), often there's only two. 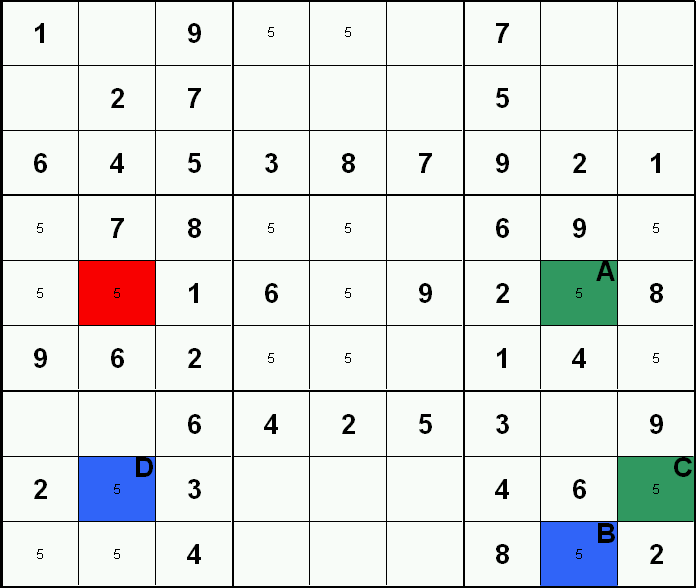Solving with Colors Of interest are candidates which are in only one of two cells in a given group (a row, column or block). Those two cells have a 'conjugate' relationship where one must be the value (true) while the other must not (false). Because we don't yet know which is which, a recognised strategy to visualise this relationship is to use two colors (and I've arbitrarily chosen blue and green). Typically there are a number of 'conjugate pairs' present at any given time. Sometimes these conjugate pairs link with other conjugate pairs forming a chain of alternate true/false cell states, and may expose candidates which can be excluded safely. Whenever two cells in a conjugate chain have the same color and also share the same group, that color must be the 'false' color since each group can only have one of any value. Also, whenever a candidate outside the chain relates by column, row or block to two alternately colored cells in a conjugate chain, that 'non-chain' candidate can be excluded. This is best understood by looking at the example. Filtering has been applied so only candidate 5's are visible. The cells labeled A & B form a conjugate pair as they are the only candidate 5's in column eight. Cells labeled B & C also form a conjugate pair as they are the only candidate 5's in the bottom right 3x3 box. Finally, cells C & D form a conjugate pair as they are the only candidate 5's in row eight. As these three conjugate pairs all link together by separate conjugate relationships, they form a chain and can be colored alternately as shown. The red marked cell remotely relates to linked conjugate pairs of alternate colors (cells A & D). Since one color must represent the true value 5, this remote candidate can safely be excluded. Credits Idea and Programming Michael Lanser Graphics Markus Lanser Music and SoundFX Frank Schlick Translation Stefan Geese, Stefanie Kloss, Sébastien Ligez Betatest Dieter Groppé, Oliver Eschbach, Heinz Süss Copyright 2006 by Silicon Wizards